Let us learn about the WQL Query SMS Units Changes after the SCCM CB 1710 Upgrade. One of my colleagues reported that their custom queries were not working as expected after the SCCM 1710 upgrade.
They have a production query to clean up devices with less than 2048 MB disk space, but it stopped working as expected after the SCCM CB 1710 upgrade. This pose will reveal more details of the WQL Query and “SMS Units” Changes after the SCCM CB 1710 Upgrade.
The changes also affect SQL views, but I don’t see any direct impact on SCCM clients and infrastructure. I agree that these changes are more logical, as the Hard Disks are coming in GBs and TBs in size.
I didn’t notice this change in my previous video post, “Differences Between SCCM ConfigMgr CB 1710 and 170. I didn’t notice this change6“.
Table of Contents
What is a WQL Query? – WQL Query SMS Units Changes after SCCM CB 1710 Upgrade
You can use the WQL query to access WMI data from the system. WMI was introduced with Windows 2000. In layman’s language, WMI is the database that stores data about Windows resources like software and hardware. SCCM collection queries are based on WQL.
- Create MS Edge SCCM Device Collection using WQL Query
- Create SCCM Windows 10 21H1 Device Collection Using WQL Query ConfigMgr | Endpoint Manager
- SCCM WQL Query Results Preview Tool | Best One to Analyze Performance of Collections
What is SMS_Units?
SMS_Units is the string that informs the Inventory Agent to perform a conversion between data provided by WMI into a form SMS can handle. The following example is valid until SCCM CB 1710 is released. Once you upgrade to 1710 then, these Megabytes will change to Gigabytes.
Example: SMS can’t handle 64-bit integers, so in the case of disk size, we use the qualifier: SMS_Units(“Megabytes“) and the agent will translate the raw # of bytes returned by WBEM into the appropriate representation in megabytes.
What is Changed in SCCM CB 1710?
As per the Microsoft SCCM product team’s updated documentation, the SCCM CB 1710 release has a revision with Inventory default units (SMS_units).
“As devices now include hard drives with sizes in the gigabyte (GB), terabyte (TB) and larger scales, this release changes the default unit (SMS_Units) used in many views from megabytes (MB) to GB. For example, the v_gs_LogicalDisk.FreeSpace value now reports GB units.”
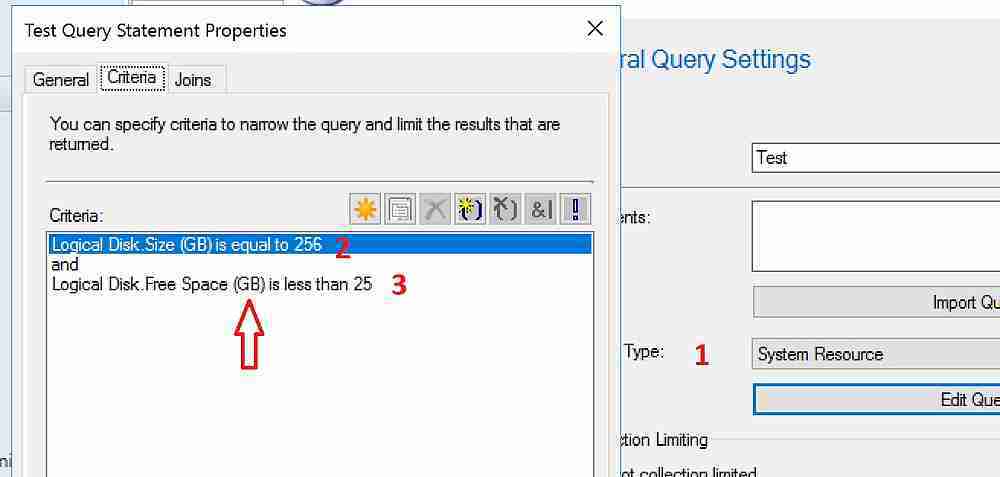
SMS_Units(“Gigabytes“) are used in different views, and we should take care of those views to notice the differences. Below is one of the sample WQL query samples. This WQL query example includes new changes in SMS_Units.
select * from SMS_R_System inner join SMS_G_System_DISK on SMS_G_System_DISK.ResourceID = SMS_R_System.ResourceId inner join SMS_G_System_LOGICAL_DISK on SMS_G_System_LOGICAL_DISK.ResourceID = SMS_R_System.ResourceId inner join SMS_G_System_PC_BIOS on SMS_G_System_PC_BIOS.ResourceID = SMS_R_System.ResourceId inner join SMS_G_System_PROCESS on SMS_G_System_PROCESS.ResourceId = SMS_R_System.ResourceId where SMS_G_System_LOGICAL_DISK.Size = 256 and SMS_G_System_PROCESS.PeakVirtualSize = 10 and SMS_G_System_PC_BIOS.BIOSVersion > “1.0” and SMS_G_System_LOGICAL_DISK.FreeSpace < 25
Values Changed in WQL Query after SCCM CB 1710 Upgrade
Let’s discuss the Values Changed in the WQL Query after the SCCM CB 1710 Upgrade. The screenshot below helps you show more details.
| Values Changed in WQL Query after SCCM CB 1710 Upgrade |
|---|
| Example WQL Query Crieria/s which I checked |
| Object Type ==> System Resource |
| Criterion Type ==> Simple Value |
| Where ==> Logical Disk – Size (GB) |
| Where ==> Logical Disk – Free Space (GB) |
| Where ==> Process – Peak Virtual Size (GB) |
We are on WhatsApp now. To get the latest step-by-step guides, news, and updates, Join our Channel. Click here. HTMD WhatsApp.
Author
Anoop C Nair is Microsoft MVP from 2015 onwards for consecutive 10 years! He is a Workplace Solution Architect with more than 22+ years of experience in Workplace technologies. He is a Blogger, Speaker, and Local User Group Community leader. His main focus is on Device Management technologies like SCCM and Intune. He writes about technologies like Intune, SCCM, Windows, Cloud PC, Windows, Entra, Microsoft Security, Career etc…

I noticed this recently after 1710 upgrade as we had created a report which pulls drive size and available size information which was earlier in MB and now changed to GB. But there is one problem, for few drives it is showing on GB and for few it is showing in MB. For ex- if server have 5 drives, 1 is showin size in MB and other 4 in GB. What can be the issue? Can you help?
I have the same problem, within view v_GS_LOGICAL_DISK, I can see some disks still using MB unit, most of the others disks are now in GB. SCCM is showing correctly everything in GB so I guess there should have somewhere the unit used for the resourceid. Anybody has an idea ?
Yes, Some disks are still using MB as all your clients are not upgraded to SCCM CB 1710 version (my assumption). I assume, once all your SCCM clients are upgraded to the latest version of CB then, you would be able to see only GB.
Does that make sense?
My mistake, even SCCM client is not displaying correctly the disks for which the capacity is still saved in MB in the database. I don’t think it is something about the client deployed because for the server in example all the disks are correctly in GB and only one is still in MB. It’s probably an issue with the refresh of the value of that disk.
Microsoft has rollback the changes on 1806
https://docs.microsoft.com/en-us/sccm/core/plan-design/changes/whats-new-in-version-1806#bkmk_bigint
I am on build 1806 and my still show MB in the resource explorer. However the values are a mix of GB and MB. All my agents are the 1806 build, and Hardware inventory has be ran across the board. What do you have to do for these values to be consistent.