Don’t try to delete Windows.OLD folder from Windows 10 device via Windows Explorer. You won’t be able to remove Windows. Old folder via Windows Explorer.
I have tried to delete this folder via Windows Explorer many times but have never succeeded. In this post, we will see the method for Deleting the Windows.OLD Folder from a Windows 10 Device.
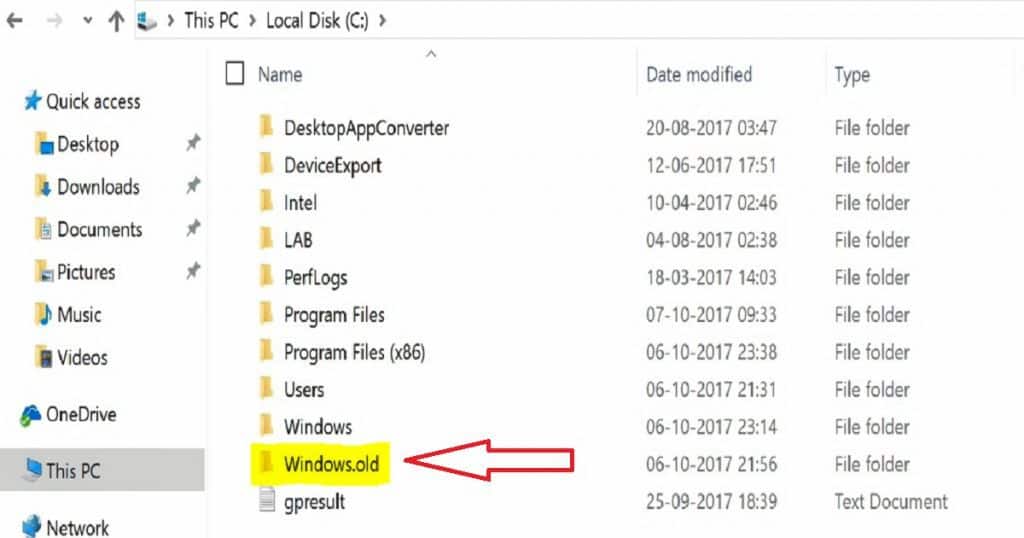
The Windows.OLD folder is where the previous installation Windows version is stored. It is created when we upgrade from one version of Windows 10 to another.
For example, when you perform an in-place upgrade of Windows 10 1703 to Windows 10 1709, the Windows.OLD folder will be created.
Table of Contents
- How to Share Files Folders on Network in Windows 11
- Find Folder Locations Using RUN Command in Windows
- Turn On or Off File Explorer Check Boxes to Select Files Folders in Windows 11
- Windows 11 Version Numbers Build Numbers
How to Remove Clean Delete Window.OLD Folder from Windows 10 Machine
In this post, you will get all the details on how to delete Windows.OLD folder. Free up C drive space. Don’t try to delete by right-clicking on Windows.OLD folder and delete. It won’t work very well.
What is there in Windows.OLD Folder?
I will give you the answer to this question depending on your answer to the following question: Are you planning to restore the device’s previous version of Windows 10?
Is it Safe to Delete Windows.OLD Folder from Windows 10 Device?
For example, If you have upgraded to Windows 10 1709 and want to restore the previous version of Windows 10 (1703), In this scenario, you need to have the Windows.OLD folder. Otherwise, you won’t be able to restore your device to the previous version of Windows 10.
How to Free up More Space in the C Drive of a Windows 10 Machine?
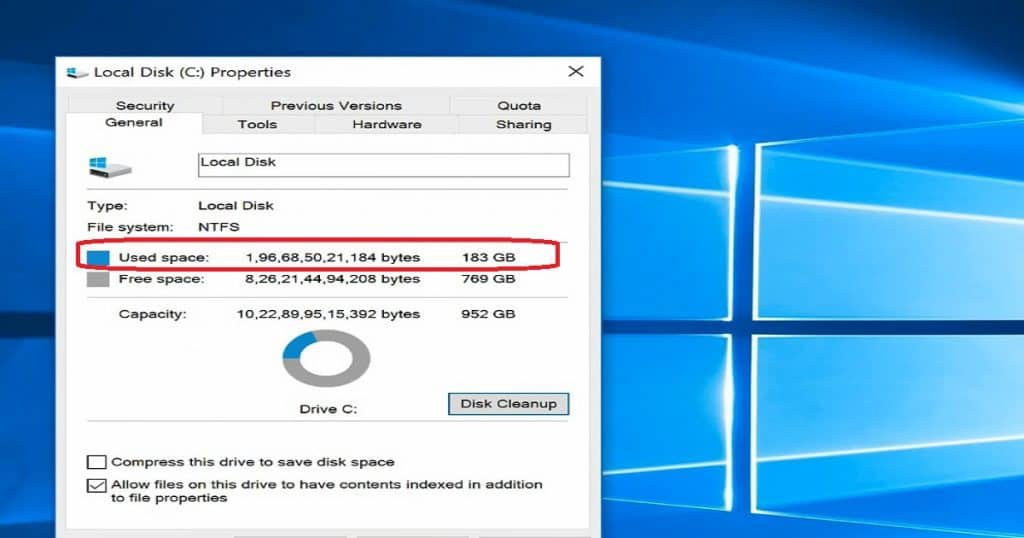
Check whether you have a folder named Windows.OLD in C drive. If so, you can remove or delete that Windows.OLD folder to get more free space on your C drive. You should get around 25 GB of free space on your Windows 10 machine’s C drive.
How to Clean-up / Delete / Remove Windows.OLD Folder from Windows 10 Device?
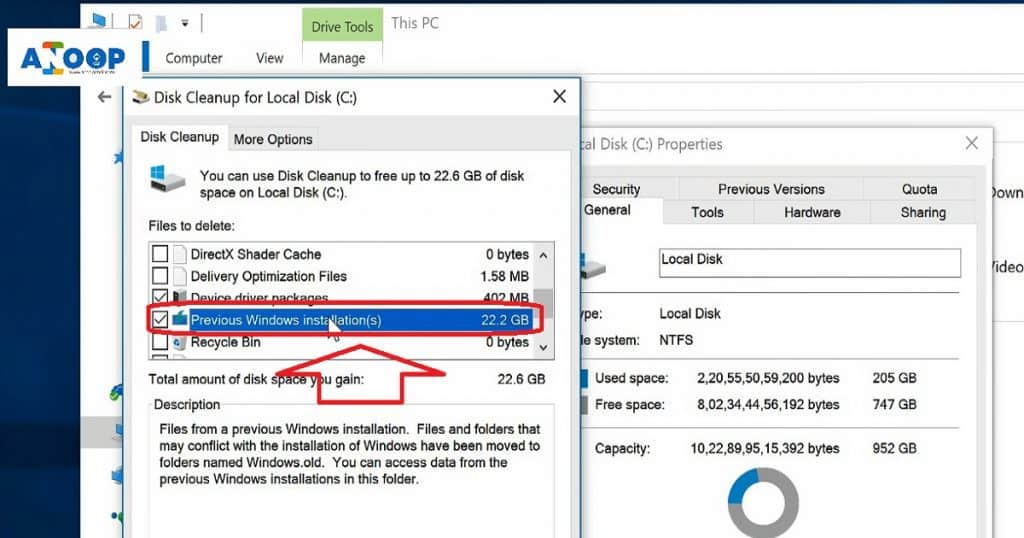
Open Windows Explorer, Click “This PC,” Right-click on the C drive, and go to properties. In the properties of the C drive, click the Disk Cleanup button.
Disk Cleanup doesn’t have an option to delete the previous installation of Windows 10, so the “previous installation of Windows” option doesn’t appear in the Disk Cleanup option.
Windows.OLD folder contains the System Files of Windows 10. Hence, we need to click on the “Cleanup System Files” button to get the option to delete Windows.OLD folder. Select “Previous Windows Installation(s)” to free up 22.2 GB of space on the C drive. Click on the OK button to start deleting the Windows.OLD folder from the C drive.
Will Windows Automatically Delete the Windows. Old Folder?
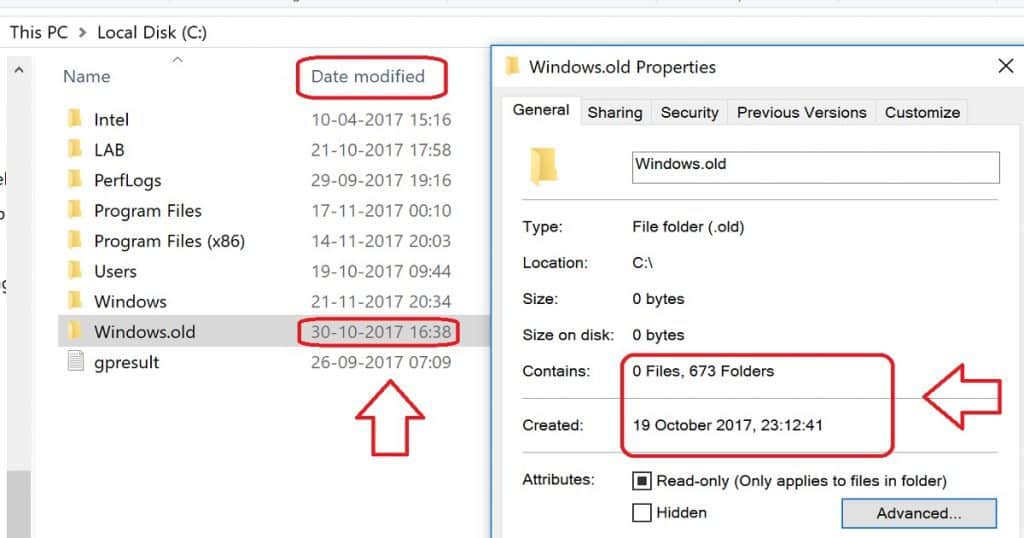
Windows won’t delete the Windows old folder. I tested this on my production machine after the Fall Creator Update of Windows 10. The content of Windows. The old folder has been removed, and the folder is zero sizes, but the Windows. The old folder is still present.
Do you want to delete the folder manually? There is no need to do that because it is not beneficial. Per my testing, this clean-up action occurred 11 days after the folder’s creation date.
| Windows .old Properties | Details |
|---|---|
| Contains | 0 Files and 673 Folders |
| Created | 19th October 2017 |
More details about the programmatic way to remove WIndows.OLD is explained here.
We are on WhatsApp now. To get the latest step-by-step guides, news, and updates, Join our Channel. Click here. HTMD WhatsApp.
Author
Anoop C Nair is Microsoft MVP! He is a Device Management Admin with more than 20 years of experience (calculation done in 2021) in IT. He is a Blogger, Speaker, and Local User Group HTMD Community leader. His main focus is on Device Management technologies like SCCM 2012, Current Branch, and Intune. He writes about ConfigMgr, Windows 11, Windows 10, Azure AD, Microsoft Intune, Windows 365, AVD, etc.

So is there a way to automate that in SCCM?