Troubleshoot Windows Autopilot Issues with MDM Diagnostics Tool

Let’s check how to Troubleshoot Windows Autopilot Issues with MDM Diagnostics Tool Windows Autopilot Issues. Let’s discuss Windows MDM Diagnostics Tool benefits, usage, and examples in this post.

In my previous post, Windows Autopilot Troubleshooting basics, we discussed different troubleshooting areas like Network Activity, Registry, and Event Viewer.

[Related Posts – Windows Autopilot Step by Step Guides, Windows 10 Deployment Process Flow and Logs]

What is Windows MDM Diagnostics Tool?

MDM Diagnostics is a command-line tool that can collate Windows Autopilot related events. Most Windows Autopilot-related events, registries, and logs are consolidated into a single folder or single file.

This tool helps IT Admins focus on one consolidated source for troubleshooting.

What are the Benefits of the MDM Diagnostics Tool?

Let’s understand how to troubleshoot Windows Autopilot Issues with MDM Diagnostics Tool as the first step, then understand its benefits.

• Automatically collect predefined logs and save them as zipping or Cab files.

• Remote users to run the command and share the logs with IT to troubleshoot.

• Use the Pre or Post OOBE stage of Windows Autopilot.

How to Use MDM Diagnostics Tool

How to use the Windows MDM diagnostics tool? I recommend using the latest Windows 10 (1803 or later) version of the MDM Diagnostics tool. I have not tested the previous version of Windows 10 with this MDM diag tool.

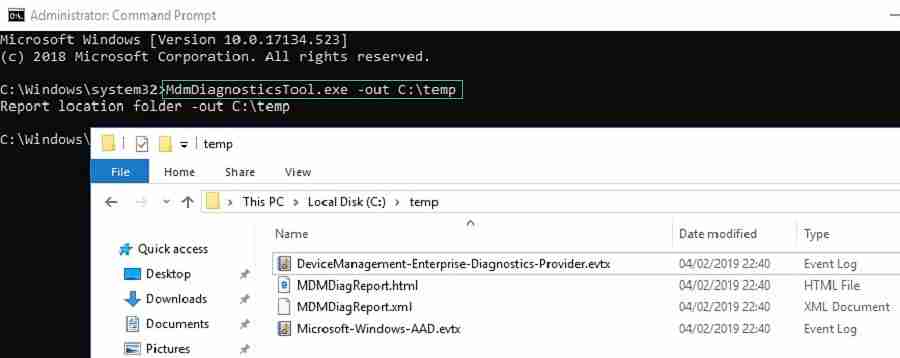
Usage 1: Syntax: MdmDiagnosticsTool.exe -out < output folder path >

Example: MdmDiagnosticsTool.exe -out c:\temp

Usage 2: Syntax: MdmDiagnosticsTool.exe -area <area name(s)> -cab <output cab file path>

Execute below command line to collect Windows autopilot related events from the system for troubleshooting.

Example: MdmDiagnosticsTool.exe -area Autopilot -cab C:\LOGS.zip

3 (Three) Troubleshooting Areas of MDM Diagnostics Tool

THE Windows MDM Diagnostics tool can be used below 3 (three) troubleshooting areas to collect pre-defined areas and logs. But, in this post, we will focus only on Windows Autopilot.

1. Autopilot
2. DeviceProvisioning
3. TPM

[Related Posts – Windows Autopilot Step by Step Guides, Windows 10 Deployment Process Flow and Logs]

The output of the MDM Diagnostics Tool

The diagnostics tool generates output in ZIP / CAB file format with the below files. We will go through each of the down output files and their purpose.

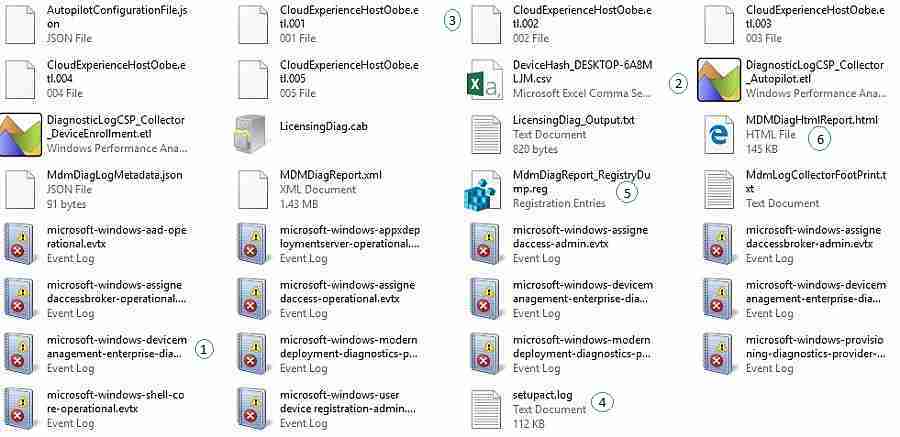
Deep Dive – Troubleshoot Windows Autopilot Issues with MDM Diagnostics Tool

You can understand more details about MDM Diagnostic tools in this section. Hopefully, the following troubleshooting steps will help you in Windows Autopilot deployment scenarios.

Event Viewer

MDM Diagnostics tool collects the below list of the event viewer. Event viewer includes client-side events like Autopilot events, policy actions, etc.

• Microsoft-windows-aad-operational
• devicemanagement-enterprise-diagnostics-provider
• microsoft-windows-assignedaccess-admin
• microsoft-windows-assignedaccess-operational
• microsoft-windows-moderndeployment-diagnostics-provider-autopilot
• microsoft-windows-provisioning-diagnostics-provider-admin
• microsoft-windows-shell-core-operational
• microsoft-windows-user device registration-admin

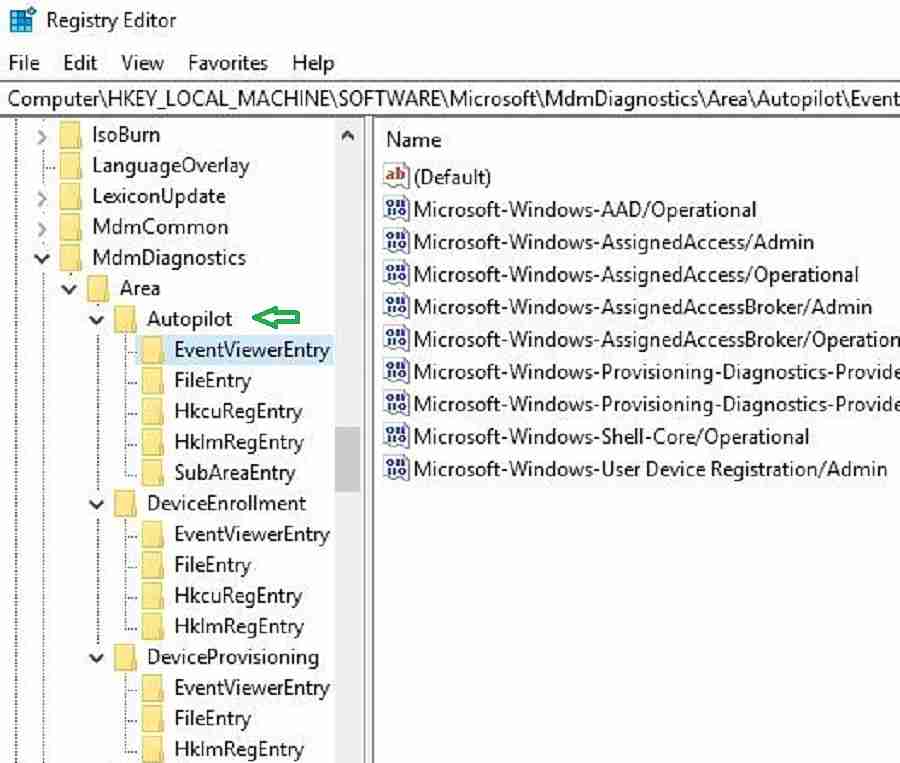
The below registry entries tells you a list of event viewer logs captured by the MDM Diagnostics tool.

Computer\HKEY_LOCAL_MACHINE\SOFTWARE\Microsoft\MdmDiagnostics\Area\Autopilot\EventViewerEntry 

Diagnostic Logs – Autopilot and Device Provisioning

The below-listed ETL files are captured by the tool. What is ETL? It’s an Event tracing log created by Windows. This tool is used for in-depth analysis of the events.

The below ETL file will include system activity captured during Autopilot and Intune device provisioning stage.

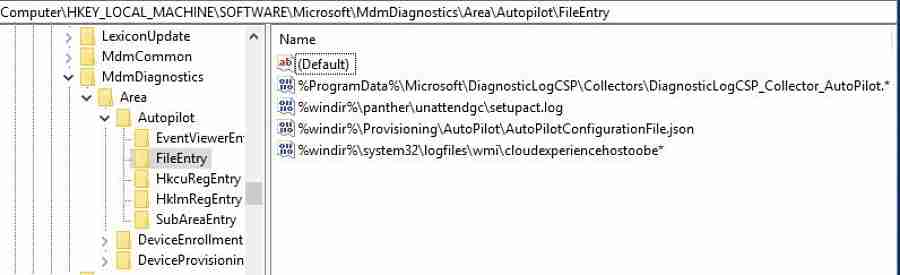
• DiagnosticLogCSP_Collector_Autopilot.etl
• DiagnosticLogCSP_Collector_DeviceProvisioning.etl

Computer\HKEY_LOCAL_MACHINE\SOFTWARE\Microsoft\MdmDiagnostics\Area\Autopilot\FileEntry

You need to use the Windows performance analyzer tool to deep dive and analyze these ETL files.

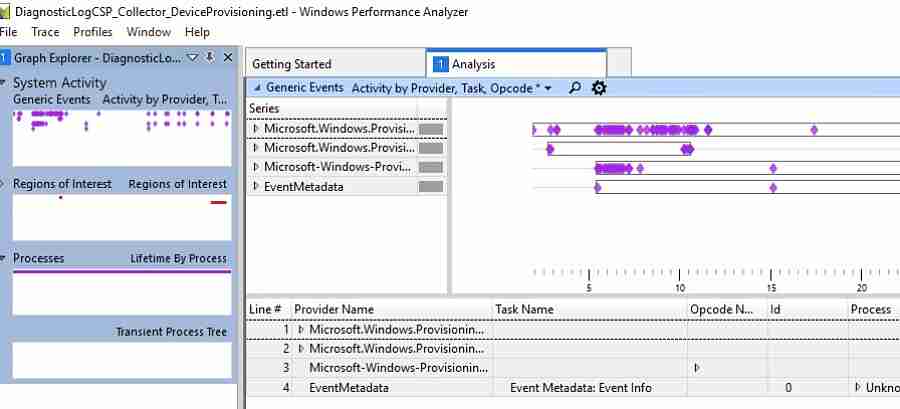
CloudExperienceHostOobe Windows Autopilot logs

Where is the location of CloudExperienceHost? It is part of system apps within the c:\windows\systemapps folder.

In Windows Autopilot deployment, the CloudExperienceHost process communicates with Azure.

To trace CloudExperienceHost process activity, MDM Diagnostics Tool generates Event Tracing Logs (ETW – Event Tracing for Windows). You can use a Windows performance analyzer to analyze the log, as shown below.

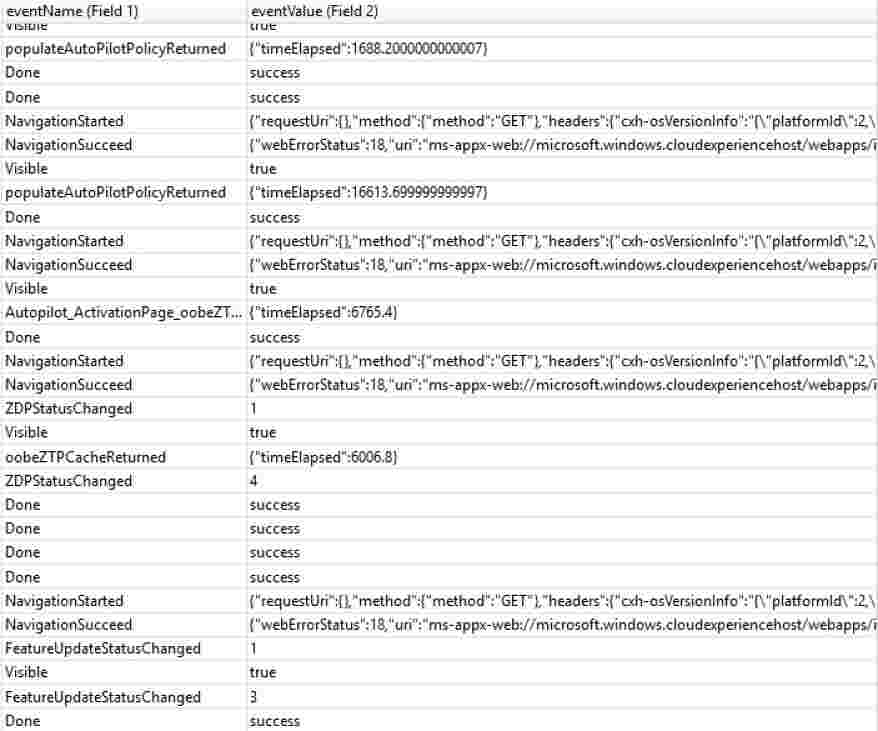
Setupact.log

This log file records actions or activity during the OOBE Phase of Autopilot.

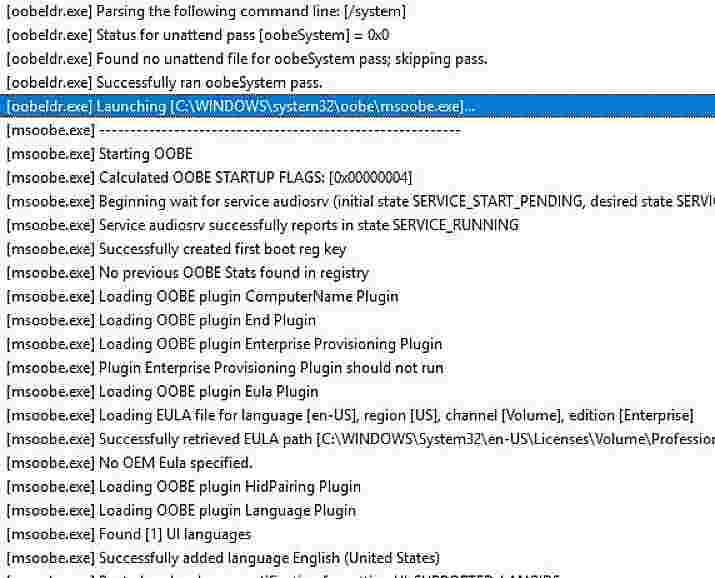
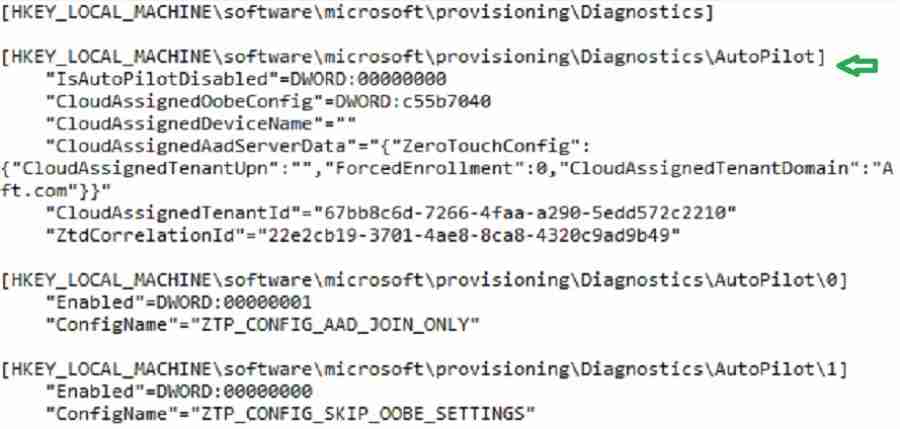
Registry Dump

MdmDiagReport_RegistryDump.reg captures the HKLM and HKCU registry values associated with autopilot device provisioning.

Autopilot related values are written to HKLM\SOFTWARE\Microsoft\Provisioning\Diagnostics\AutoPilot

Intune CSP based configurations are written to HKEY_LOCAL_MACHINE\software\microsoft\policymanager\

MDMDiag Report

MDMDiagReport.xml report provides resultant Autopilot settings applied from Intune.

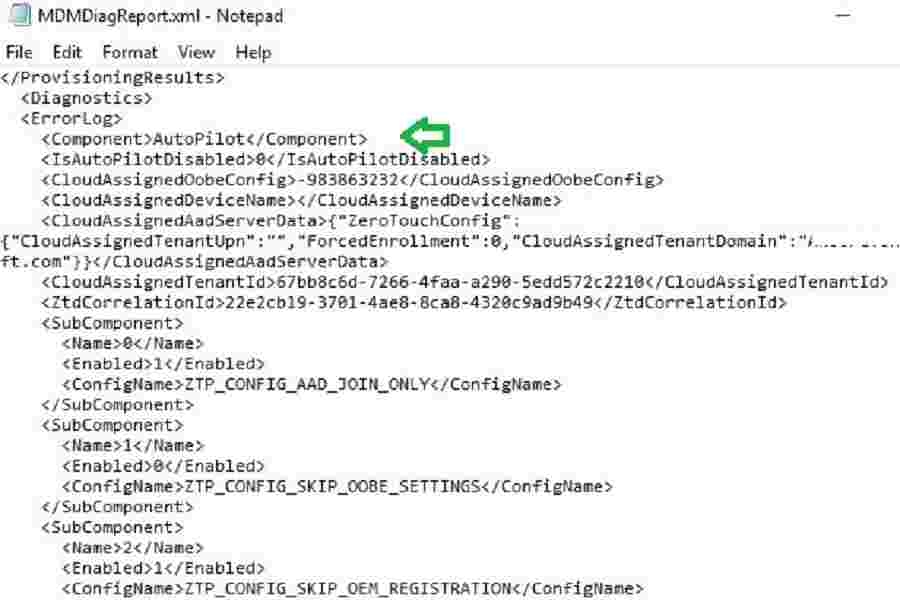
MDMDiagHtmlReport.html report provides complete details on the applied Intune Policy CSP Settings, certificates, applications, etc., on the autopilot device.

Resources

• Windows Autopilot Deployment Scenarios – On-Prem Hybrid Domain Join
• Step by Step Guide Windows AutoPilot Process with Intune 
• Beginners Guide Setup Windows AutoPilot Deployment 
• Windows Autopilot Video Starter Kit

Author

Vimal has more than ten years of experience in SCCM device management solutions. His main focus is on Device Management technologies like Microsoft Intune, ConfigMgr (SCCM), OS Deployment, and Patch Management. He writes about the technologies like SCCM, Windows 10, Microsoft Intune, and MDT.